2007年公务员考试《行测》卷

2007年浙江公务员考试《行测》卷

一、数量关系，共25题，参考时限30分钟，本部分包括数字推理、数理计算。

1、0.5，2，9/2，8，(     )。

A、12.5

B、27/2

C、14+1/2

D、16

2、100，8，1，1/4，(      )。

A、1/4

B、1/12

C、1/20

D、1/32

3、85，52，(      )，19，14。

A、28

B、33

C、37

D、41

4、1，6，30，(      )，360。

A、80

B、90

C、120

D、140

5、0，9，26，65，(      )，217。

A、106

B、118

C、124

D、132

6、243，217，206，197，171，(      )，151。

A、160

B、158

C、162

D、156

7、36，24，(      )，32/3，64/9。

A、431/27

B、140/9

C、49/3

D、16

8、5，7，4，9，25，(      )。

A、168

B、216

C、256

D、296

9、(      )，35，63，80，99，143。

A、24

B、15

C、8

D、1

10、3，18，60，147，(      )。

A、297

B、300

C、303

D、307

11、1²⁰⁰⁷+3²⁰⁰⁷+5²⁰⁰⁷+7²⁰⁰⁷+9²⁰⁰⁷的值得个位数是：

A、5

B、6

C、8

D、9

12、把圆的直径缩短20%，则其面积将缩小：

A、40%

B、36%

C、20%

D、18%

13、小张在做一道除法时，误将除数45看成54，结果得到的商是3，余数是7。

问正确的商和余数之和是： 

A、11

B、18

C、26

D、37

14、把自然数1，2，3，4，5，，98，99 分成三组，如果每组数的平均数刚好相等，那么此平均数为：

A、55

B、60

C、45

D、50

15、某部队战士排成了一个6行、8列的长方阵。现在要求各行从左至右1，2，1，2，1，2，1，2报数，再各列从前到后1，2，3，1，2，3报数。

问在两次报数中，所报数字不同的战士有： 

A、18个

B、24个

C、32个

D、36个

16、同时扔出 A、B 两颗骰子（其六个面上的数字都为1，2，3，4，5，6），问两个骰子出现的数字的积为偶数的情形有几种：

A、27种

B、24种

C、32种

D、54种

17、A、B两地相距100公里，甲以10千米/小时的速度从A地出发骑自行车前往B地。6小时后，乙开摩托车从A地出发驶向B地。问为了使乙不比甲晚到B地，麾托车每小时至少要行驶多少千米：

A、24千米

B、25千米

C、28千米

D、30千米

18、如下图所示，梯形ABCD，AD∥BC，DE⟂BC，现在假设AD、BC的长度都减少10%，DE的长度增加10%，则新梯形的面积与原梯形的面积相比，会怎样变化：

A、不变

B、减少 1%

C、增加 10%

D、减少 10%

19、某单位实行五天工作制，即星期一至星期五上班，星期六和星期日休息。现已知某月有31天，且该单位职工小王在该月休息了9天（该月没有其他节日），则这个月的六号可能是下列四天中的哪一天：

A、星期五

B、星期四

C、星期三

D、星期一

20、如图所示，长方形ACEG被线段BF、HD分成四个大小不等的小长方形。已知AH为6cm，GF为3cm，DE为10cm，BC为7cm，则三角形ICG的面积为：

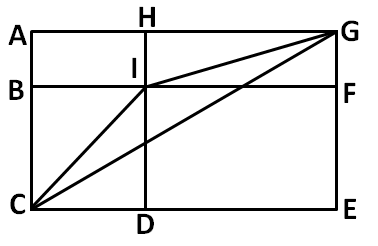
A、32cm²

B、28cm²

C、30cm²

D、26cm²

21、某代表团有756名成员，现要对A、B两议案分别进行表决，且他们只能投赞成票或反对票。已知赞成A议案的有476人，赞成B议案的有294人，对A、B两议案都反对的有169人，则赞成A议案且反对B议案的有：

A、293人

B、297人

C、302人

D、306人

22、如下图所示，矩形ABCD的面积为1，E、F、G、H分别为四条边的中点，FI的长度是IE的两倍，问阴影部分的面积为多少：

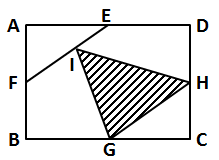
A、1/3

B、1/4

C、5/16

D、7/24

23、先将线段AB分成20等份，线段上的等分点用“△”标注，再将该线段分成21等份，等分点用“Ο”标注（A、B两点都不标注），现在发现“△”和“Ο”之间的最短处长为2厘米，问线段AB的长度为多少：

A、2460 厘米

B、1050 厘米

C、840 厘米

D、680 厘米

24、林子里的猴子喜欢吃的野果，23只猴子可以在9周内吃光，21只猴子可以在12周内吃光，问如果有33只猴子一起吃，则需要几周吃光（假定野果生长的速度不变）：

A、2 周

B、3 周

C、4 周

D、5 周

25、某工程由小张、小王两人合作刚好可在规定的时间内完成。如果小张的工作效率提高20%，那么两人只需用规定时间的9/10就可完成工程；如果小王的工作效率降低25%，那么两人就需延迟2.5小时完成工程。

问规定的时间是多长： 

A、20小时

B、24小时

C、26小时

D、30小时