2018年特岗教师招聘考试《中学数学》试题

2018年四川省特岗教师招聘考试《中学数学》试题

一、单项选择题。下列各题备选答案中只有一项符合题意，请将其选出。（共12小题，每小题4分，共48分）

1、已知集合A={-1，0，1，2}，集合B={x|x≥0}，则集合A∩B=（  ）。

A、∅

B、{-1}

C、|1，2}

D、{0，1，2}

2、下列函数为奇函数的是（  ）。

A、y=cosx

B、y=x²

C、y=lnx+x

D、1/x

3、设i为虚数单位，则复数(1-i)/i=（  ）。

A、-1-i

B、1-i

C、-1+i

D、1+i

4、为了解某地区中小学生的诗词量，从该地区中小学中抽取部分学生进行调查，事先已经了解到该地区小学、初中、高中三个学段学生诗词量差异较大，男女诗词量差异不大。下面的抽样方法中，最适合的是（  ）。

A、简单随机抽样

B、按性别分层抽样

C、按学段分层抽样

D、系统抽样

5、已知在正项等比数列{an}中，a₇*a₁=256，则a₄=（  ）

A、8

B、16

C、32

D、256

6、若一个几何体的三视图都是三角形，则该几何体是（  ）。

A、圆锥

B、圆台

C、三棱锥

D、三棱台

7、某筒羽毛球有5个球，其中有2个不合格，其余均合格。那么从中随机抽出2个球，抽到羽毛球均合格的概率为（  ）。

A、1/10

B、3/10

C、6/10

D、7/10

8、若直线x+y-2=0与圆x²+(y-a)²=2相交，则实数a的取值范围是（  ）。

A、<0，4>

B、（0，4）

C、（-∞，4）

D、（-∞，4）∪（4，+∞）

9、函数f（x）=sin2x（cos²x-sin²x）是（  ）。

A、最小正周期为π/2的奇函数

B、最小正周期为π/2的偶函数

C、最小正周期为π的奇函数

D、最小正周期为π的偶函数

10、设a，b∈R则“a=2”是“直线x+2y-b=0与直线x+ay+3=0平行”的（  ）。

A、充分不必要条件

B、必要不充分条件

C、充分必要条件

D、既不充分也不必要条件

11、设x，y∈R，a1，b>1，若a^x=b^y=2，a+b=2√2，则1/x+1/y的最大值为（  ）。

A、8

B、3

C、2

D、1

12、营养学家指出，成人良好的日常饮食应该至少提供0.075kg的碳水化合物，0.06kg的蛋白质，0.06kg的脂肪。1kg食物A含有0.105kg的碳水化合物，0.07kg的蛋白质，0.14kg的脂肪，花费28元，而1kg食物B含有0.105kg碳水化合物，0.14kg的蛋白质，0.07kg的脂肪，花费21元。为了满足营养学家指出的日常饮食要求，最低需要花费的成本为（  ）。

A、14元

B、16元

C、19元

D、20元

二、填空题。根据题干内容，在横线中填写正确答案。（共4小题，每小题4分，共16分）

13、若平面向量，向量a=（m，1），向量b=（-1，3），且向量a垂直向量b，则m=。

14、log₂4-2log₉3=。

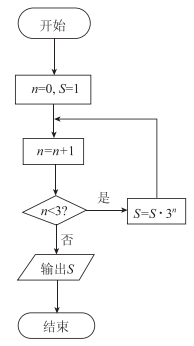
15、程序如图所示，S=。

16、(sinθ+cosθ)/(sinθ-cosθ)=-3，则tan2θ=。

三、解答题。根据题目要求，回答问题。（共5小题，第17-20题每题7分，第21题8分，共36分）

17、等差数列{a_n}满足a₁+a₃=6,a₂+a₄=10。
（1）求数列{a_n}的通项公式；
（2）已知数列{a_n}的前n项和为S_n，若a₁，a_k，S_k+4，（k∈N*）成等比数列，求k的值。

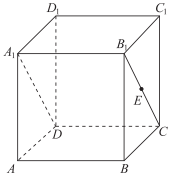
18、如图所示，正方体ABCD-A₁B₁C₁D₁的棱长为1，E为B₁C上一点
（1）若E为线段B₁C的中点，求证：A₁D⊥平面AED₁；
（2）求三棱锥A-DED₁的体积。

19、△ABC的内角A，B，C所对的边分别为a，b，c，已知sin(B-C)+2sinCcos B-2sinB=0
（1）求a/b的值；
（2）已知b=1，sinB=√15/8，求c。

20、已知抛物线C：y²=2px，其准线l过点（-1，2），焦点为F。
（1）求抛物线C的准线方程；
（2）点P(x₀，y₀)在抛物线C上，且以点F为圆心，以|FP|为半径的圆与直线l相切，求点P的坐标。

21、已知函数f（x）=e²-ax-2，其中a>0，e=2.71828……为自然对数的底数。
（1）讨论函数f（x）的单调性；
（2）是否存在a，使得f（x）>-1在x∈R上恒成立？若不存在，请说明理由；若存在，求出a的取值范围。

       注：本试题来源于考生回忆及网络仅供参考！（金标尺教育收集整理）