2016年四川特岗教师招聘考试《小学数学》试题及解析
一、选择题(本大题共15小题,每小题3分,共45分)
1、 已知集合P={x∣x2-x-2≤0),Q={x∣log2(x-1)≤1),则(CRP)∩Q等于()
A、(-∞,-1]∪[3,+∞)
B、[2,3]
C、(-∞,-1]∪(3,+∞)
D、(2,3]
2、反比例函数f(x)=k/x(k为常数)的图像如右图所示,下列说法正确的是( ).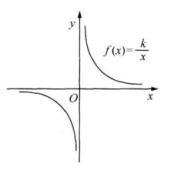
A、常数k<-1
B、函数f(x)在定义域范围内,y随x的增大而减小
C、若点a(-1,m)和点b(2,n)在函数f(x)的图像上,则m<n
D、函数f(x)图像的对称轴的直线方程是y=x
3、计算(2+i)(1-i)2/(1-2i)=( )
A、2
B、-2
C、2i
D、-2i
4、若sinθcosθ>0,则θ在( ).
A、第一、二象限
B、第一、三象限
C、第一、四象限
D、第二、四象限
5、在△ABC中,三边a,b,c成等差数列,√a,√b,√c也成等差数列,则△ABC是( ).
A、正三角形
B、等腰三角形
C、直角三角形
D、钝角三角形
6、设不等式 表示的平面区域为D,在区域D内随机抽取一个点,则此点到坐标原点的距离大于2的概率是( ).
表示的平面区域为D,在区域D内随机抽取一个点,则此点到坐标原点的距离大于2的概率是( ).
A.π/4
B.(π-2)/2
C.π/6
D.(4-π)/4
7、在平面直角坐标系中,设A(-2,3),B(3,-2,)沿x轴把直角坐标系折成120°二面角后,则AB的长度是( ).
A.√2
B.3√2
C.2√11
D.4√2
8、将直线x+y=1先绕点(1,0)顺时针旋转90°,再向上平移1个单位后,与圆x2+(y-1)2=r2相切,则半径r的值是( ).
A.√2/2
B.√2
C.3√2/2
D.1
9、双曲线x2/a2-y2/b2=1的右准线与两渐近线交于A、B两点,右焦点为F,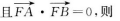 双曲线的离心率为( ).
双曲线的离心率为( ).
A.2√3/3
B.√3
C.√2
D.2
10、(√x+1)4(x-1)5展开式中,x4的系数为( ).
A、-10
B、10
C、40
D、45
11、若a+1=b(a和b是不为0的自然数),那a和b的最小公倍数是( )
A、a
B、b
C、ab
D、(a+1)b
12、在平面直角坐标系中,点P(-4,5)关于原点对称的点的坐标为( ).
A、(4,5)
B、(4,-5)
C、(-4,-5)
D、(5,-4)
13、下列性质中,等腰三角形具有而直角三角形不一定具有的是( ).
A、两边之和大于第三边
B、有一个角的平分线垂直于这个角的对边
C、有两个锐角的和等于90°
D、内角和等于180°
14、一个无盖的正方体盒子的平面展开图可以是图中的( ).
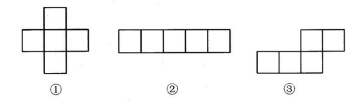
A、①
B、①②
C、②③
D、①③
15、若命题甲是命题乙的充分不必要条件,命题丙是命题乙的必要不充分条件,命题丁是命题丙的充要条件,则命题丁是命题甲的( ).
A、充分不必要条件
B、必要不充分条件
C、充要条件
D、既不充分也不必要条件
二、填空题(本大题共5小题,每小题3分,共15分)
16、已知直线l过点A(0,2),且倾斜角的正切值为1,则直线l的方程为 .
17、已知正方体的棱长为1,则这个正方体的外接球的直径为 .
18、在等差数列{an}中,若a3=3,a5=7,则a7= .
19、一个锐角的补角比这个角的余角大 度.
20、已知函数f(x)=12/x+3x(x>0),则f(x)的最小值为 .
三、简答题(本大题共5小题.每小题8分.共40分.解答应写出文字说明.证明过程或演算步骤)
21、在△ABC中,角A,B,C所对的边分别是a,b,C且满足csinA=acosC.
(1)求角C的大小;
(2)求√3sinA-cos(B+π/4) 的最大值,并求取得最大值时角A、B的大小.
22、如图,在正方体ABCD-A1B1C1D1中,棱长AA1=2,E为CC1的中点。
(1) 求证:B1D1 ⊥AE;
(2) 求二面角C-AE-B的平面角的正切值;
(3) 求点D1到平面EAB的距离.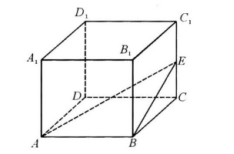
23、等差数列{an}的公差不为零,a4=7,以a1,a2,a5成等比数列。
(1)求{an}的通项公式;
(2)若数列{Tn}满足Tn=a2+a4+a8+ …+a2n,求Tn。
24、如图所示,一次函数y=kx+b的图像与反比例函数y=m/x的图像交于A(1,2),B(-m,-1)两点.
(1)求反比例函数和一次函数的解析式;
(2)根据图像直接写出使一次函数的值大于反比例函数的值的x的取值范围.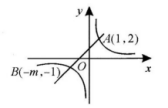
25、义务教育数学课程标准在各个学段都安排了数与代数的学习内容。小学生在第二学段将进一步学习整数、分数、小数和百分数及有关运算,进一步发展数感,假如你是小学第二学段的数学教师,你在教学中将会从哪些方面去培养学生的数感?(至少写出三个方面的观点)

 地区
地区 考试科目
考试科目 微信
微信

 微博
微博 抖音
抖音 023-67417095
023-67417095

















 点击关注
点击关注










