2015年四川特岗教师招聘考试《小学数学》试题
一、选择题(本大题共15小题,每小题3分,共45分)
1、已知集合A={-1,0,1},集合B={x∣x2+x=0},则集合A∪B=( )。
A、{-1,0,1}
B、{-1,0}
C、{0,1}
D、{-1,1}
2、函数f(x)=x2的图像关于( ).
A、y轴对称
B、直线y=x对称
C、坐标原点对称
D、直线y=-x对称
3、若向量a=(2,6),向量b=(3,x),且a∥b,则x=( )。
A、-1
B、1
C、4
D、9
4、若角α的终边在第二象限,则点P(sinα,cosα)在( )·
A、第一象限
B、第二象限
C、第三象限
D、第四象限
5、函数f(x)=2的x次方+3x的零点所在的一个区间是( )·
A、(-2,-1)
B、(-1,0)
C、(0,1)
D、(1,2)
6、下列函数中,在区间(0,+∞)上为减函数的是( ).
A、y=2x
B、y=lnx
C、y=√x
D、y=1/x
7、设i为虚数单位,则复数(3+i)/(1+i)=
A、-1-i
B、-2+i
C、2-i
D、2+i
8、有两张卡片,一张的正反面分别写着数字1与2,另一张的正反面分别写着3与4,将两张卡片排在一起组成一个两位数,则所组成的两位数为奇数的概率是( ).
A、1/4
B、1/3
C、1/2
D、3/4
9、已知三棱锥的底面是边长为1的正三角形,其正视图如图所示,则此三棱锥的体积为( )
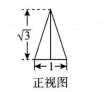
A、1/4
B、√3/6
C、√3/4
D、3/4
10、双曲线x2/2-y2=1的离心率是( ).
A、√3/2
B、√5/2
C、√6/2
D、2
11、为了得到函数y=sin(x+π/3)的图像,只需把函数y=sinx的图像上所有的点( ).
A、向左平移π/3个单位长度
B、向右平移π/3个单位长度
C、向上平移π/3个单位长度
D、向下平移π/3个单位长度
12、圆(x-1)2+y2=1的圆心到直线x+y-2=0的距离是( ).
A、1/2
B、√2/2
C、√3/2
D、1
13、若正实数x和y满足x+2y=1,则xy的最大值是( ).
A、1/2
B、1/4
C、1/8
D、1/16
14、抛物线y2=4x上一点P到点F(1,0)的距离是3,则点P到y轴的距离为( ).
A、1
B、2
C、3
D、4
15、若α、β为两个不同的平面,m为平面α上一条直线,则“α⊥β”是“m⊥β”的( ).
A、充分不必要条件
B、必要不充分条件
C、充要条件
D、既不充分也不必要条件
二、填空题(本大题共5小题,每小题3分.共15分)
16、lg2+lg5= .
17、一支田径队有男运动员28人,女运动员21人,现按性别用分层抽样的方法,从中抽取14位运动员进行健康检查,则男运动员应抽取 人.
18、执行如图所示的程序框图,输出的S的值是 .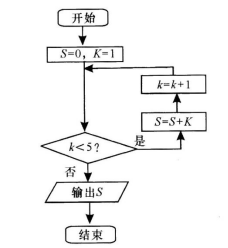
19、已知sinα-cosα=√2,则sin2α= .
20、设变量x,y满足约束条件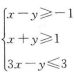 ,则目标函数z=4x+y的最大值为 .
,则目标函数z=4x+y的最大值为 .
三、解答题(本大题共5小题,每小题8分,共40分.解答应写出文字说明,证明过程或演算步骤)
21、已知△ABC的内角A、B、C所对的边分别为a、b、C,cosA=√5/5,cosB=√10/10,c=1
(Ⅰ)求cosC的值;
(Ⅱ)求△ABC的面积.
22、已知公差不为0的等差数列{an}的首项为2,且a1、a2、a4成等比数列.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设数列{an}的前n项和为Sn,求数列{Sn/n}的前n项和.
23、在正方体ABCD-A1B1C1D1中,点M、N分别是棱AB、C1D1的中点.
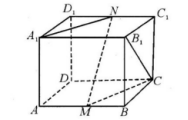 (Ⅰ)证明:直线MN⊥直线B1C;
(Ⅰ)证明:直线MN⊥直线B1C;
(Ⅱ)证明:直线CM∥平面AA1N。
24、已知点P是椭圆x2/4+y2/3=1上的一点,点F1,F2是该椭圆的焦点。
(Ⅰ)求△PF1F2的周长;
(Ⅱ)若△PF1F2的面积是3/2,求点P的坐标。
25、已知函数f(x)=lnx。
(Ⅰ)求函数f(x)的图像在x=1处的切线方程;
(Ⅱ)证明:f(x)≤x/e(e为自然对数的底数).
注:本试题来源于考生回忆及网络仅供参考!(金标尺教育收集整理)

 地区
地区 考试科目
考试科目 微信
微信

 微博
微博 抖音
抖音 023-67417095
023-67417095

















 点击关注
点击关注










