2017年湖北省农村义务教育学校教师招聘考试《中学数学》
一、单项选择题(本大题共15题,每题2分,共30分。下列每题给出的四个选项中只有一个选项是最符合题目要求的。请在“答题卡”上将所选项的字母涂黑)
1、在Rt△ABC中,∠C=90°,若cosA=3/5,则tanB的值是( )。
A、3/5
B、3/4
C、4/5
D、4/3
2、下图是由六个棱长为1的正方体组成的几何体,其主视图的面积是( )。

A、3
B、4
C、5
D、6
3、男子跳高的15名运动员的成绩如下表所示:

根据表中数据可以判断这些运动员成绩的中位数、众数分别是( )。
A、1.70,1.75
B、1.70,1.80
C、1.65,1.75
D、1.65,1.80
4、已知集合A={-2,1,2},B={x|x2-x-2=0},则A∩B=( )。
A、∅
B、{2}
C、{1}
D、{-2}
5、在等差数列{an}中,a1=2,a3+a5=16,则a7=( )。
A、8
B、12
C、14
D、16
6、我国古代《易经》一书中记载,远古时期人们通过在绳子上打结来记录数量,即“结绳计数”。如图,一位母亲在从右到左依次排列的绳子上打结,满七进一,用来记录孩子自出生后的天数,由图可知,孩子自出生后的天数是( )。
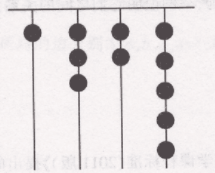
A、83
B、335
C、509
D、1325
7、某天早上小明上学,先步行一段路,因为时间紧,他又改乘出租车,结果到校还是迟到了5分钟,其行程情况如图,若出发时直接乘出租车(车速不变),则他( )。

A、刚好按时到校
B、仍会迟到2分钟到校
C、可以提前5分钟到校
D、可以提前2分钟到校
8、如图,点P为⊙O上一动点,PA,PB为⊙O的两条弦,BE,AF分别垂直于PA,PB,垂足分别为E,F,若∠P=60°,⊙O的半径为4,则EF的长( )
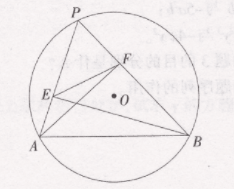
A、随P点运动而变化,EF的最小值为2√3
B、随P点运动而变化,EF的最大值为2√3
C、等于2√3
D、随P点运动而变化,EF的值无法确定
9、命题“若x≤-2,则x2≥4”的逆否命题是( )。
A、若X2≤4,则x≥一2
B、若x2<4,则x>-2
C、若x2≥4,则x≤-2
D、若x2>4,则x<-2
10、在yOz平面上的直线z=y绕z轴旋转一周之后得到的曲线方程为( )。
A、z2=x2+y2
B、x2=y2+z2
C、x2+y2-z2=1
D、x2+y2-z2=-1
11、

A、A
B、B
C、C
D、D
12、已知函数f(x)在区间(0,1)内可导,则以下结论正确的是( )。
A、f(x)在x=0处一定连续
B、f(x)在x=0处左导数一定存在
C、f(x)在x=1/2处一定可微
D、f(x)在x=1处一定可导
13、在某教师设计的“一次函数的图象和性质”的教学目标中,“在一次函数图象及性质的探究过程中.养成联系实际、善于观察、勇于探索和勤于思考的习惯”属于以下四个方面中的( )。
A、知识技能
B、数学思考
C、问题解决
D、情感态度
14、二次方程、二次不等式、二次函数在教材中是分别研究的,为了将以上概念统一起来并从更高的角度加以认识.我们主要通过( )。
A、方程思想
B、函数思想
C、演绎思想
D、递推思想
15、以下是某学生证明勾股定理“在Rt△ABC中,∠C=90°,求证a2+b2=c2”的过程:因为a=csinA,b=ccosA,所以a2+b2=c2sin2A+c2cos2A=c2(sin2A+cos2A)=c2。
以上证明所犯的错误主要是( )。
A、偷换论题
B、虚假论据
C、循环论证
D、不能推出
二、填空题(每小题3分,共5小题,共15分)
16、一个盒子内装有大小、形状相同的四个球,其中红球1个、绿球1个、白球2个,小明摸出一个球不放回,再摸出一个球,则两次都摸到白球的概率是__________。
17、如图,Rt△ABC中,AB=6,BC=4,∠B=90°,将△ABC折叠,使A点与BC的中点D重合,折痕为MN,则线段BN的长为__________。
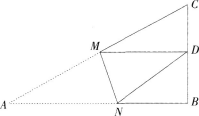
18、在平面直角坐标系中,点(2,2)到直线x+2y-2=0的距离为__________。
19、f(x)=x2,则f´(x)在x=2处的导数值为__________。
20、《义务教育数学课程标准(2011年版)》指出数据分析是统计的核心,数据分析的过程可以概括为收集数据、__________、__________、__________。
三、解答题(共4小题,每题6分,共24分)
21、在△ABC中,内角A,B,C所对的边分别为a,b,c,a=4,b=5,c=√21。
(1)求cosC的值;
(2)求△ABC的面积。
22、某商场要经营一种新上市的文具,进价为20元/件,试营销阶段发现,当销售单价是25元时,每天的销售量是250件;销售单价每上涨1元,每天的销售量就减少10件。
(1)直接写出商场销售该文具每天所得的销售利润形(元)与销售单价x(元)之间的函数关系式:
(2)求销售单价为多少元时,该文具每天的销售利润最大。
23、已知曲线y=ex与直线y=c(c>1)及Y轴所围成的平面图形的面积为1,求实数c的值。
24、已知随机变量X在(0,5)上服从均匀分布,求方程4X2+4Xx+X+2=0有实根的概率?
四、综合题
25、什么是概念的内涵与外延,举例说明它们之间的关系。
26、运算能力是《义务教学数学课程标准(2011版)》提出的一个核心概念,培养学生的运算能力的基本途径有哪些?
27、为帮助学生形成“整式的加减”中“同类项”的概念.某教师在给出同类项的定义之前设计了以下的问题序列:
问题1:你能说出下列各式的结果吗?
①3个苹果+5个苹果;②6张书桌-2张书桌;③9亿-4亿。
问题2:你能否解决“3个苹果+2张书桌=?”这样的问题?
问题3:你能写出下列式子的结果吗?

问题4:你能写出下列式子的结果吗?
①4a+5a;②7ab-2ab;③3a2b-5a2b;④2a+3b;⑤4ab-7a2b;⑥9x2y3-4x3y2。
问题5:你能用一两句简明的话,概括下列两组式子所反映的特征吗?
①4a与5a,7ab-2ab,3a2b与-5a2b;
②2a与3b,4ab与-7a2b,9x2y3与-4x3y2。
(1) 该教师提出问题2和问题3的目的分别是什么?
(2) 试分析该教师设计该问题序列的作用。
注:本试题来源于考生回忆及网络仅供参考!(金标尺教育收集整理)

 地区
地区 考试科目
考试科目 微信
微信

 微博
微博 抖音
抖音 023-67417095
023-67417095

















 点击关注
点击关注










