2017年省长沙市教师招聘考试《中学数学》题

2017年湖南省长沙市教师招聘考试《中学数学》题

一、单项选择题。下列各题备选答案中只有一项符合题意，请将其选出。

1、若A={(x，y)||x+3|+√(y-1)}=0，B={-3，1}，则必有（  ）。 

A、A∩B=⊘

B、A≥B

C、A≤B

D、A=B

2、 将函数  f(x)=e^x  的图象向左平移一个单位得到图象 C₁，再将图象 C₁ 向上平移一 个单位得到 C₂，作出 C₂关于y=x的对称图象 C₃，则 C₃ 对应的函数解析式为（  ）。 

A、y=ln(x-1)+1

B、y=ln(x-1)-1

C、y=ln(x+1)+1

D、y=ln(x+1)-1

3、为使方程x²+(a+2i)x+3+ai=0（i是虚数单位）至少有一个实数根，则实数 a 的 取值为（  ）。

A、a≥4

B、a≤-4

C、a≥4或a≤-4

D、a=±2√3

4、 若存在实数 a，b使得me^x-x≤0 的解集为[a，b]，则 m 的取值范围是（  ）。 

A、(1/e²，e）

B、(0，1/e²)

C、(1/e²，1/e)

D、(0，1/e)

5、已知定义在R 上的奇函数f(x)的周期为3，若f(-1)=0，则在区间(0，6)内满足f(x)=0的解至少有（  ）个。 

A、4

B、5

C、6

D、7

6、由x=e，y=2x  及曲线y=2/x所围成的封闭图形的面积为（  ）。

A、3+ln2

B、e²-3

C、3

D、e

7、 点F为双曲线x²/a²-y²/b²=1(a>0，b>0)的焦点，过点 F的直线与双曲线的一条渐近线 垂直交于点 A，与另一条渐近线交于点 B，若向量AF与向量BF的比值为1：4，则双曲线的离心率是（  ）。 

A、2√6/3

B、√6/3

C、2√3/3

D、√5/2

8、 已知正方体ABCD-A₁B₁C₁D₁ 的棱长为 6，E是AB的中点，点P是面BB₁C₁C上的 一动点，其满足∠DPC=∠EPB，则三棱锥P-ABC体积的最大值为（  ）。 

A、36

B、12√3

C、24

D、18√3

9、对方程4x|x|+9y|y|+36=0有如下叙述：①x 与 y 具有函数关系；②x+y≤0； ③当x≥0时，y≤-2；④ y 可能随 x 的增大而增大；⑤点（x，y）不会在第一象限。其 中论断错误的个数是（  ）。 

A、4

B、3

C、2

D、1

10、如图是一个算法的程序框图，若此程序运行结果为 S=3，则在判断框中应填入关 于 i 的判断条件是（  ）。

A、i≤7

B、i≤8

C、i≤9

D、i≤10

二、填空题。根据题干内容，在横线中填写正确答案。

11、在△ABC中，若2sinA+cosB=2，sinB+2cosA=√3，则∠C的大小应为。

12、已知实数 x，y 满足不等式组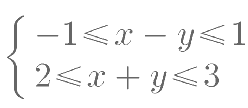

，则z=x+2y的取值范围为          。 

13、在Rt△ABC中，已知D 为斜边AB 的中点，点P 在线段CD 上，且满足|CP|=|PD|，则(|PA|²+|PB|²)/|PC|²=            。

三、解答题。根据题目要求，回答问题。

（一）

某项闯关挑战赛设有 A，B 两个关卡，A，B 关卡依次进行，只有闯过关卡 A，才 能进入关卡 B，A，B 关卡均有 2 次挑战机会，现有人参与挑战，其顺利通过关卡 A 的概2/3，其顺利通过关卡 B 的概率是1/2，假设各次挑战互不影响。

14、求其顺利闯关的概率； 

15、假设其不放过每次机会，记参加挑战的次数为ξ，求ξ的数学期望E_ξ。

（二）

已知在四棱锥P-ABCD中，底面ABCD为矩形，AD=2，AB=1，PA⊥平面ABCD，E，F 分别是线段AB，BC的中点，G为PA上的点，且PG=3GA。

16、证明：PF⊥FD；

17、证明：EG∥平面PDF。

18、若PA=1，求二面角A-PD-F的余弦值。

（三）

已知数列{a_n}中，a₁=1，a_n+1=2a_n/(a_n+2)，(n∈N*)。

19、求数列{a_n}的通项公式；

20、设b_n=(n∈N*)。数列 {b_n} 的前 n 项和为 Sn，求证2√(n+1)-1<Sn<2√n，(n∈N*)。

（四）

 已知函数 f（x）=xln x+1。

21、求函数 f（x）的单调区间；

22、对一切x∈(0，+∞），2f(x)≤3x²+2ax+3 恒成立，求实数a的取值范围。

（五）

已知抛物线 C：y²=4x的焦点为 F，过点F的直线l与抛物线C交于A、B 两点，过点K(-1，0）与点A的直线l’与抛物线 C 相交于另一点 D。

23、求证：B、D 关于 x 轴对称；

24、若作 AB 的垂直平分线与抛物线 C 交于 M、N 两点，以 MN 为直径的圆恰好经过 A、B 两点，求直线 l 的方程。

注：本试题来源于考生回忆及网络仅供参考！（金标尺教育收集整理）