2017年娄底市市直学校教师招聘考试《小学数学》试题及答案

2017年娄底市市直学校教师招聘考试《小学数学》试题及答案

一、单项选择题(本大题共8小题，每小题3分。共24分)

1、如图，某公司A，B，C三个住宅区在同一条直线上，公司所有员工分别住在三个小区内，A区有20人，B区有25人，C区有40人，该公司的接送车打算在此三个住宅区只设一个停靠点．为使员工步行到停靠点的路程之和最小．那么停靠点的位置应设在()。

A、B区

B、C区

C、A区

D、A、B、C三个区都可以

2、一个R里有黄豆、绿豆若干粒，若取出2粒黄豆，则绿豆是剩下黄豆的7/8；若取出2粒绿豆，囊黄豆与囊下的绿豆之比是7：6，那么盒子里原有的绿豆比黄豆少()。

A、1/8

B、1/7

C、2/13

D、2/15

3、如图,D是△ABC内的一点，BD⊥CD，AD=6，BD=8，CD=6，E，F，G，H分别是AB，AC，CD， BD的中点．则四边形EFGH的周长是()。

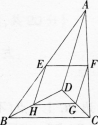
A、12

B、14

C、15

D、16

4、质地均匀的骰子六面分别刻有1-6的点数，掷两次骰子，得到向上一面的两个点数，则下列事件中，发生可能性最大的是()。

A、点数都是偶数

B、点数的和为奇数

C、点数的和小于10

D、点数的和大于7

5、把浓度为15％和浓度为40％的两种糖水混合，要配制成140克浓度为30％的糖水，15％的糖水需取()克。

A、84

B、8.4

C、56

D、3.6

6、某科学家设计了一面时钟，这面时钟每时100分钟，每天10时。当这面时针显示5时时，实际是标准时间中午12时。则这一天实际标准时间晚上8时24分，在这面时钟上显示的是()。

A、4时90分

B、8时40分

C、7时50分

D、8时50分

7、如图，面积为20的正方形ABCD中，有一个小正方形EFGH，其中E，F，G分别在AB，BC，FD上，若BF=√5/2，则小正方形的周长是()。

A、5√5/8

B、5√5/6

C、5√5/2

D、10√5/3

8、定义[a，b，c]为函数y=ax²+bc+c的特征数，下面给出特征数为[ 2m ，1-m，-1-m]的函数的一些结论：

①当m=-3时，函数图象的顶点坐标是{1/3,-(8/3)}；

②当m>0时，函数图象截石轴所得的线段长度大于3/2；

③当m<0时，函数在x>1/4时，y随x的增大而减小；

④当m≠0时，函数图象经过同一个点。

其中正确的结论有()。

A、②③④

B、①②④

C、③④

D、②④

二、填空题(本大题共10小题，每小题2分，共20分)

9、用n个棱长是a cm的小正方体可以摆出“一”字形长方体，如图，n个小正方体拼在一起 时，这个长方体表面积是_______cm²。

10、如图，已知图中四边形两条边的长度和三个角的度数，四边形ABCD的面积是______cm²

11、如图，在矩形ABCD中，AB=5，BC=12，将矩形ABCD沿对角线对折放在桌面上，折叠后所成的图形覆盖桌面的面积是______。

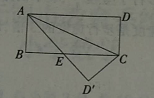
12、时钟原来表示的时间是7点整，时针转了82．5º后，现在的时刻是______。

13、一个圆锥的高不变，底面半径比原来减少25%，则原来的体积比现在多( )/( )。

14、

15、方程√x+√y=√18的整数解有______组。

16、已知x2=x+1，y2=y+1，且x≠y，则x3+y3=______。

17、如图，边长为a的正方形ABCD中，点E是对角线BD上的一点，且BE=BC，点P在EC上，PM⊥BD于M，PN⊥BC于N，则PM+PN=________。

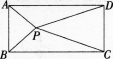
18、如图，P是矩形ABCD内一点，若PA=3，PB=4，PC=5，则PD=_______。

三、计算题(本大题共4小题。每小题5分，共20分)

19、

20、某人每天早上7：10从家出发，匀速步行到单位上班，正好按时到达。有一天因事耽误，7：30 才从家出E。为赶时间，他跑步行了全程3/4，剩下的路程他仍按以前的步行速度前进，结果他正好按时到达。已知他跑步的速度是步行速度的3倍，请你根据以上信息计算出他原来每天步行到单位上班要多少分钟?

21、一个圆柱形容器，从里面量，底面直径为4 dm，高5 dm。容器中装有一些水，深27 cm现在在容器中放入一个底面半径为1dm，高4 dm的圆柱体铁棒，把铁棒垂直于容器底面，竖直放在容器中，容器中水面上升多少cm?

22、已知关于x的方程x2-2(k-1)x+k2有两个实数根x1，x2。

(1)求k的取值范围；

(2)若|x1-x2|=x1x2-1，求k的值。

四、解答题(本大题共2小题。每小题8分。共16分)

23、秋冬之际，由于天气逐渐变冷，牧场上的草以固定的速度在减少。已知一个牧场上的草可供45头牛吃4天或可供25头牛吃6天。照此计算，这个牧场可供几头牛吃10天?

24、如图，已知圆⊙O是△ABC的外接圆，AD是圆⊙0的直径，且BD=BC，延长AD到E，且有∠EBD=∠CAB。

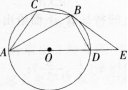
(1)求证：BE是⊙0的切线；

(2)若BC=√3，AC=5，求圆的直径AD及切线BE的长。

五、综合题【本大题共2小题，每小题l0分，共20分)

25、一个书架上有上、中、下三层，共藏书1920。现从上层取出本层藏书数的7/11放入中层，接着从中层取出本层现有藏书数的3/7放入下层，最后从下层取出本层现有藏书数的1/3放入上层．这时三层的藏书本数刚好相等。求原来上、中、下三层各藏书多少本?

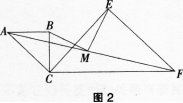
26、已知两个共用一个顶点的等腰Rt△ABC，等腰Rt△CEF，∠ABC=∠CEF= 90º，连接AF，M是AF的中点，连接MB，ME。

(1)如图1，当CB与CE在同一直线上时，若CB=a，CE=2a，求BM，ME的长；

(2)如图2,当∠BCE=45º时，求证：BM=ME。

注：本试题来源于考生回忆及网络仅供参考！（金标尺教育收集整理）