2021年4月10日省教师招聘考试《初中数学》题

2021年4月10日江西省教师招聘考试《初中数学》题

一、单项选择题。本大题一共50道题，每道题目1分，共50分。

1、课程标准（2011年版）中，课标提出了总体目标和具体目标，具体目标为（  ）。

A、知识技能、数学思考、解题能力、应试能力

B、数学思考、问题解决、运算能力、情感态度

C、知识技能、数学思考、问题解决、情感态度

D、问题解决、解决能力、运算能力、应试能力

2、课程标准（2011年版）指出“综合与实践”是指一类以问题为载体，以学生自主与为主的学习活动，其教育价值为（  ）。

A、有助于学生的发展

B、有助于学生对数学的全面理解

C、有助于教师的发展

D、有助于课程的建设

3、教学设计因遵循的原则有系统性原则、（  ）、可行性原则、反馈性原则。

A、科学性原则

B、程序性原则

C、主动性原则

D、启发性原则

4、评价既要关注学生数学学习的水平，也要重视学生在数学活动中所表现出来的（    ）。

A、情绪与态度

B、情感与情绪

C、态度与习惯

D、情感与态度

5、数学教学活动要注重培养学生良好的（  ），使学生掌握恰当的数学学习方法。

A、数学思考方法

B、数学思考能力

C、数学学习习惯

D、数学学习能力

6、新课程的核心理念是（  ）。

A、联系生活学数学

B、培养学生的学习兴趣

C、掌握知识培养能力

D、为了每一位学生的发展

7、新课程提倡的三维教学目标是指（  ）。

A、知识、技能和方法

B、情感、态度和价值观

C、知识、技能和情感

D、知识与技能、过程与方法和情感态度和价值观

8、从探究活动中了解学生独立思考的习惯和（  ）的意识。

A、合作交流

B、自主探究

C、自主学习

D、动手实践

9、“知识与技能”既是学生发展的基础性目标，又是落实数学思考、问题解决和情感态度目标的（  ）。

A、前提

B、基础

C、联系

D、载体

10、教师在基本技能的教学中，不仅要使学生掌握技能操作的程序和步骤，还要使学生理解程序和步骤的（  ）。

A、方法

B、道理

C、特点

D、结构

11、已知3^a=10，9^b=5，则3^a-2b的值为（  ）。

A、5

B、1/2

C、2/5

D、2

12、如果4+√5与4-√5的小数部分分别是m，n，那么m+n-1的值为（  ）。

A、7

B、1

C、0

D、-1

13、一组数据4，5，5，6，若添加一个数据5，则发生变化的统计量是（  ）。

A、平均数

B、众数

C、中位数

D、方差

14、如果a，b，c满足a²+2b²+2c²-2ab-2bc-6c+9=0，则abc等于（  ）。

A、9

B、27

C、54

D、81

15、两个正五边形按如图所示的方式摆放，若∠1=30°，则∠2 =（  ）。

A、45°

B、42°

C、35°

D、30°

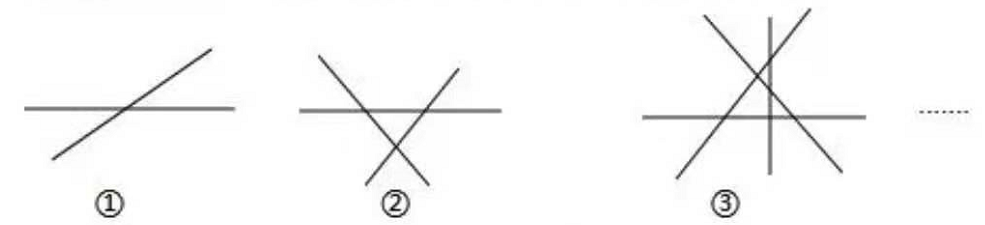
16、观察如图并阅读图形，下面的相关数字，两条线相交，最多有个交点，三条线相交，交点最多有个交点，条线相交，最多有个交点······，像这样条直线相交，交点最多的个数是（  ）。

A、100个

B、135个 

C、190个 

D、200个

17、物体的形状如图所示，则从上面看此物体得到的平面图形是（  ）。

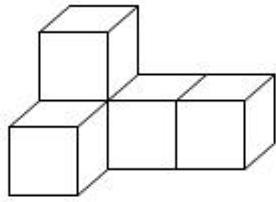
A、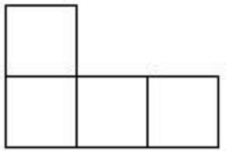

B、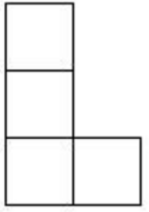

C、

D、

18、如果m-n=1，那么代数式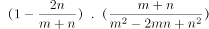的值（  ）。

A、-3

B、-1

C、1

D、3

19、如图，已知AD∥BC，∠C=30°，∠ADB:∠BDC=1:2。那么∠ADB等于（  ）。

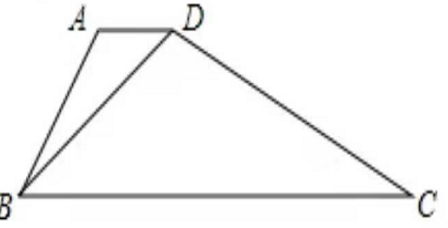
A、45°

B、30°

C、50°

D、36°

20、下列说法中：

①两个全等三角形一定成轴对称。

②等腰三角形的对称轴是底边上的中线。

③等边三角形一边上的高所在的直线就是这边的垂直平分线。

④一条线段可以看作是以它的垂直平分线为对称轴的轴对称图形。

正确的有（  ）。

A、1个

B、2个

C、3个

D、4个

21、如图，RtΔABC中，∠ACB=90°，∠BAC=30°。∠ACB的角平分线与∠ABC的外角平分线交于E点，连接AE，∠AEB的度数是（  ）。

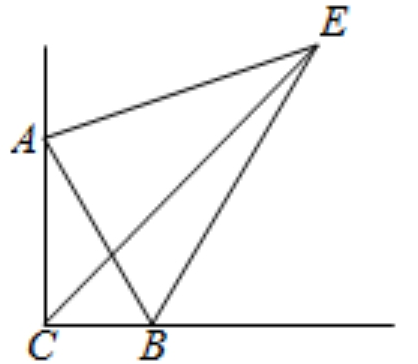
A、30°

B、40°

C、45°

D、35°

22、若关于x的不等式组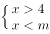无解，则的取值范围是（  ）。

A、m>4

B、m<4

C、m≥4

D、m≤4

23、已知一次函数y=kx+3的图像经过A，且y随x的增大而减小，则点A的坐标可以是（  ）。

A、（-1，2）

B、（1，-2）

C、（2，3）

D、（3，4）

24、如图，在ΔABC中，若DE∥BC，AD=3，BD=6，AE=2，则AC的长为（  ）。

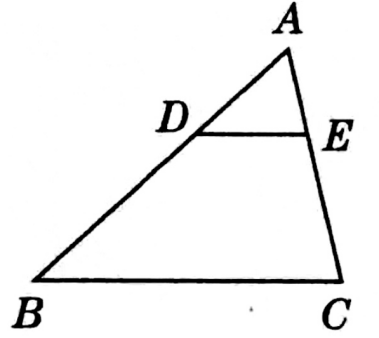
A、4

B、5

C、6

D、8

25、我国古代数学著作《增删算法统计》记载，绳索量竿问题：一条竿子一条索，索比竿子长一托，折回索子却量竿，却比竿子短一托，其大意为现有一根竿子和一条绳索，用绳索去量竿，绳索比竿子长五尺，如果将绳索对折后再去量竿，就比竿短五尺，设绳索长为x尺，则符合题意的方程是（  ）。

A、x/2=(x-5)-5

B、x/2=(x+5)+5

C、2x=(x-5)-5

D、2x=(x+5)+5

26、如图所示，同时自由转动两个转盘，指针落在每一个数上的机会均等，转盘停止后，两个指针同时落在一奇一偶上的概率是（  ）。

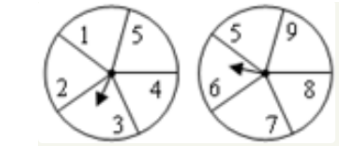
A、12/25

B、8/25

C、13/25

D、4/5

27、设A(x₁，y₁)、B(x₂，y₂）是反比例函数y=-2/x图象上任意两点，且y₁<y₂，则x₁、x₂可能满足的关系是（  ）。

A、x₁>x₂>0

B、x₁<0<x₂

C、x₂<0<x₁

D、x₂<x₁<0

28、如图，将长方形纸片ABCD沿AE折叠，使点D恰好落在BC边上点F处，若AB=6，AD=10，则EC的长为（  ）。

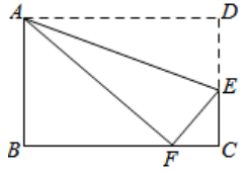
A、2

B、8/3

C、3

D、10/3

29、已知菱形的周长为8，两邻角的度数比为1:2，则菱形的面积是（  ）。

A、8√3

B、8

C、4√3

D、2√3