2021年10月30日全国教师资格证考试《初中数学》题
一、单项选择题。每题5分,共8题,共40分
1、极限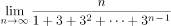 的值是( )。
的值是( )。
A、0
B、2/3
C、1
D、2
2、A、B两点分别在是x2+y2-6x+16y-48=0和x2+y2+4x-8y-44=0上运动,A、B两点距离最大值( )。
A、13
B、32
C、36
D、38
3、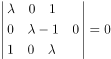 ,求⋋的值( )。
,求⋋的值( )。
A、-1或1
B、-1或2
C、0或1
D、0或2
4、已知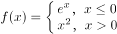 ,则f(x)在x=0处( )。
,则f(x)在x=0处( )。
A、连续
B、左连续但不右连续
C、右连续但不左连续
D、既不左连续也不右连续
5、ɑ1,ɑ2,ɑ3因为三维向量,如阵A=(ɑ1,ɑ2,ɑ3),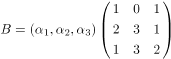 ,如若|A|=2,则|B|=( )。
,如若|A|=2,则|B|=( )。
A、2
B、6
C、12
D、14
6、已知事件A发生的概率是1/3,事件B发生的概率是1/5,事件A和事件B同时发生的概率是1/15,则事件A和事件B同时都不发生的概率是( )。
A、8/15
B、9/15
C、13/15
D、14/15
7、南宋时期数学家秦九韶在数学上的主要成就是( )。
A、二分法
B、辗转相除法
C、大衍求一术
D、割圆术
8、下列不能用尺规(无刻度的直尺和圆规)作图的是( )。
A、过一点作已知直线的垂线
B、已知底边和底边上的高作等腰三角形
C、已知斜边和直角边作直角三角形
D、作任意角的三等分线
二、简答题。每题7分,共5题,共35分
9、求曲线y=ln2x,直线x=1与x=5及x轴所围成平面区域的面积。
10、已知动点P与定点A(0,0,1)的距离等于P到平面z=4距离的一半。
(1)求动点P的轨迹方程。
(2)动点P的轨迹方程所表示的几何图形是什么?
11、不透明的袋子中有10个完全相同的乒兵球,分别标有数字1到10,从袋中随机摸出1个球,记录标号后放回袋子,再随机摸出1个球,记录标号后也放回袋中。
(1)求两次摸球的标号之和是3的概率;
(2)求两次摸球的标号之和最大是7的概率。
12、列举义务教育阶段一元二次方程的三种主要解法。
13、简述义务教育阶段统计内容中数据分析的主要过程,给出描述数据集中趋势和离散程度的统计量(各写出2个)。
三、解答题。每题10分,共1题,共10分
14、已知向量ɑ1=(4,2,-2)T,ɑ2=(4,4,0)T,ɑ3=(-3,-1,3)T,β=(4,5,-1)T。
(1)证明向量组ɑ1,ɑ2,ɑ3线性无关。
(2)将向量β用,ɑ1,ɑ2,ɑ3线性表示。
四、论述题。每题15分,共1题,共15分
15、(1)写出义务教务阶段涉及的不等式的性质(2条即可)。
(2)阐述不等式的性质与解一元一次不等式的关系,并举例说明。
五、案例分析题。每题20分,共1题,共20分
(一)
在某习题课上,老师让学生独立完成如下例题:
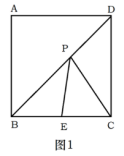
如图1,在边长为的正方形ABCD中,E是BC中点,P是对角线BD上的动点,连接PE,PC,当BP为何值时,PE+PC的值最小?最小值是多少?
大多数学生表示不会做。教师这样启发:回顾以前学过的“饮马问题”:如图2,牧马人从A地出发,到一条笔直的河边饮马,然后回到B地,牧马人到河边什么地方饮马,所走的路径最短?
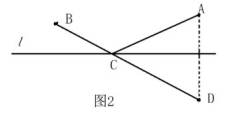
作点A关于直线的对称点D,连接BD交直线l于点C。由于AC+BC=BC+CD=BD,利用两点之间线段最短,此时点C使AC+BC最小,点c的位置即为所求。
学生:哦,会做了....
16、问题:
(1)给出该例题的求解过程。(10分)
(2)指出该教师对学生的启发有哪些合理和不足之处。(10分)
六、教学设计题。每题30分,共1题,共30分
(二)
下面是某教材有理数一章中“绝对值”一节的内容片段:
两辆汽车从同一处![]() 出发,分别向东、西方向行驶10km,到达A、B两处,它们的行驶路线相同吗?它们的行驶路程相等吗?
出发,分别向东、西方向行驶10km,到达A、B两处,它们的行驶路线相同吗?它们的行驶路程相等吗?
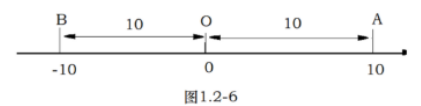
一般地,数轴上表示数a的点与原点的距离叫做数a的绝对值,记作|a|,例如,图中A、B两点分别表示10和-10,它们与原点的距离都是10个单位长度,所以10和-10的绝对值都是10,即|10|=10,|-10|=10,显然|0|=0。
由绝对值的定义可知:
一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0。即
(1)如果a>0,那么|a|=a;
(2)如果a=0,那么|a|=0;
(3)如果a<0,那么|a|=-a
根据上述内容,完成下列任务:
17、(1)写出其中蕴含的主要数学思想方法;(6分)
(2)完成“绝对值”这节课的教学设计,要求写出教学目标、教学重点和主要教学过程(含情境导入、概念理解、概念巩固)。(24分)
注:试题来源于考生回忆及网络,仅供参考!

 地区
地区 考试科目
考试科目 微信
微信

 微博
微博 抖音
抖音 023-67417095
023-67417095
















 点击关注
点击关注










