事业单位《职测》数量关系备考技巧：抽屉问题

在之前的文章中小编给大家介绍了事业单位《职测》数量关系中的常考数列汇总，今天小编给大家准备了事业单位《职测》数量关系中抽屉问题的原理及解题思路，希望对备考的小伙伴们有所帮助。

一、抽屉原理

1.抽屉原理1

将多于n件的物品任意放到n个抽屉中，那么至少有一个抽屉中的物品件数不少于2。（也可以理解为至少有2件物品在同一个抽屉）

2.抽屉原理2

将多于m×n件的物品任意放到n个抽屉中，那么至少有一个抽屉中的物品的件数不少于m+1。（也可以理解为至少有m+1件物品在同一个抽屉）

二、解题思路

1.利用抽屉原理1

【示例】有20位运动员参加长跑，他们的参赛号码分别是1、2、3、…、20，至少要从中选出多少个参赛号码，才能保证至少有两个号码的差是13的倍数？

【解析】若想使两个号码的差是13，考虑将满足这个条件的两个数放在一组，这样的号码分别是{1、14}、{2、15}、{3、16}、{4、17}、{5、18}、{6、19}、{7、20}，共7组。还剩下号码8、9、10、11、12、13，共6个。考虑最差的情况，先取出这6个号码，再从前7组中的每一组取1个号码，这样再任意取出1个号码就能保证至少有两个号码的差是13的倍数，共取出了6+7+1=14个号码。

2.利用抽屉原理2

【示例】一个口袋中有50个编上号码的相同的小球，其中编号为1、2、3、4、5的各有10个。一次至少要取出多少小球，才能保证其中至少有4个号码相同的小球？

【解析】将1、2、3、4、5五种号码看成5个抽屉。要保证有一个抽屉中至少有4件物品，根据抽屉原理2，至少要取出5×3+1=16个小球，才能保证其中至少有4个号码相同的小球。

3.利用最差原则

最差原则说的就是在抽屉问题中，考查最差的情况来求得答案。因为抽屉原理问题所求多为极端情况，故可以从最差的情况考虑。从各类公务员试题来看，“考虑最差情况”这一方法的使用广泛而且有效。

【示例】从一副完整的扑克牌中，至少抽出多少张牌，才能保证至少6张牌的花色相同？

【解析】一副完整的扑克牌包括大王、小王；红桃、方块、黑桃、梅花各13张，分别是A、2、3、4、5、6、7、8、9、10、J、Q、K。要求6张牌的花色相同，考虑最差情况，即红桃、方块、黑桃、梅花各抽出5张，再加上大王、小王，此时共取出了4×5+2=22张，此时若再取一张，则一定有一种花色的牌有6张。即至少取出23张牌，才能保证至少6张牌的花色相同。

4.与排列组合问题结合

【示例】某区要从10位候选人中投票选举人大代表，现规定每位选举人必须从这10位中任选两位投票，问至少要有多少位选举人参加投票，才能保证有不少于10位选举人投了相同两位候选人的票？

【解析】从10位候选人中选2人共有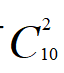=5种不同的选法，每种不同的选法即是一个抽屉。要保证有不少于10位选举人投了相同两位候选人的票，由抽屉原理2知，至少要有45×9+1=406位选举人投票。

5.与几何问题结合

【示例】在一个长4米、宽3米的长方形中，任意撒入5个豆，5个豆中距离最小的两个豆距离的最大值是多少米？

【解析】将长方形分成四个全等的小长方形（长为2米，宽为1.5米），若放5个豆的话，则必有2个豆放在同一个小长方形中，二者之间的距离不大于小长方形对角线长，因此5个豆中距离最小的两个豆距离的最大值是2.5米。

以上就是本文的全部内容，祝大家考试顺利~

推荐阅读：

事业单位有哪些

事业编事业单位报考条件要求

事业单位考试科目有哪些

事业单位考试内容

事业编制和公务员的区别

事业单位人事管理条例

事业单位联考各省试卷一样吗

事业单位联考什么意思

事业单位ABCDE类的区别是什么