事业单位《职测》数量关系备考技巧：容斥问题

在之前的文章中小编给大家介绍了事业单位《职测》数量关系中工程问题的原理及解题思路，今天小编给大家准备了事业单位《职测》数量关系中容斥问题的原理及解题思路，希望对备考的小伙伴们有所帮助。

一、容斥原理

涉及多个相互关联的集合，要求根据集合间的相互关系计算集合中元素个数的问题称为“容斥原理”问题。

二、解题思路

1.公式法解两个集合容斥问题

两个集合的容斥问题公式：

A∪B=A+B-A∩B

三个集合的容斥问题公式：

A∪B∪C=A+B+C-A∩B-B∩C-C∩A+A∩B∩C

【示例】某班有56人，每人至少参加一个兴趣小组，参加生物组的有46人，参加科技组的有28人，两组都参加的有多少人?

【解析】集合A={参加生物组的人｝、集合B={参加科技组的人｝，由A∪B=A+B-A∩B知两组都参加的有A∩B=46+28-56=18人。

2.文氏图法解两个集合容斥问题

【示例】某班参加体育活动的学生有25人，参加音乐活动的有26人，参加美术活动的有24人，同时参加体育、音乐活动的有16人，同时参加音乐、美术活动的有15人，同时参加美术、体育活动的有14人，三种活动都参加的有5人，这个班共有多少名学生参加活动？

【解析】设A={参加体育活动}、B={参加音乐活动}、C={参加美术活动}

根据题意，将所给的条件填入相应的集合中，可画出文氏图如下：

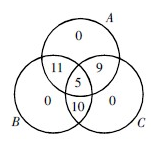
根据图示，可知全班共有11+5+9+10=35名学生参加活动。

以上就是本文的全部内容，祝大家考试顺利~

推荐阅读：

事业单位有哪些

事业编事业单位报考条件要求

事业单位考试科目有哪些

事业单位考试内容

事业编制和公务员的区别

事业单位人事管理条例

事业单位联考各省试卷一样吗

事业单位联考什么意思

事业单位ABCDE类的区别是什么