事业单位《职测》数量关系备考技巧：浓度问题

在之前的文章中小编给大家介绍了事业单位《职测》数量关系中日期星期问题的原理及解题思路，今天小编给大家准备了事业单位《职测》数量关系中浓度问题的原理及解题思路，希望对备考的小伙伴们有所帮助。

一、浓度原理

溶液就是把某种固体或者液体放入水里面，两者混在一起的产物。溶质就是放进去的那种固体或者液体，溶剂就是水。浓度就是溶质占到整个溶液的百分比，即浓度=溶质÷溶液

二、解题思路

溶液问题常见的有两种，一种是溶液的混合，这种问题用公式解决；另外一种是单一溶液的蒸发或稀释，这种题目一般用比例法解决，即利用溶质不变进行求解。

混合溶液特性：一种高浓度的溶液A和一种低浓度的同种溶液C混合后得到溶液B，那么溶液B的浓度肯定介于溶液A和溶液C的浓度之间。

1.方程法

方程法适用于大部分浓度问题，具有思维过程简单的特点。一般来说，方程法有两个要素，第一是设未知数，要求易于求解；第二是找等量关系列出方程。浓度问题中往往以浓度作为未知变量，这样等量关系易于表达，但也伴有浓度数值大部分是小数不好计算的弊病，还需要在实际做题中细加体会。

【示例】一杯含盐15%的盐水200克，要使盐水含盐20%，应加盐多少克？

【解析】设应加盐x克，则(200*15%+x)÷(200+x)=20%，解得x=12.5。

2.特值法

对于那些比例非常明确的浓度问题，我们可以用特值法来避免分数的出现，从而简化计算步骤。

【示例】两个相同的瓶子装满某种化学溶液，一个瓶子中溶质与水的体积比是3∶1，另一个瓶子中溶质与水的体积比是4∶1，若把两瓶化学溶液混合，则混合后的溶质和水的体积之比是？

【解析】1+3=4和1+4=5的最小公倍数为4×5=20，且3∶1=15∶5，4∶1=16∶4，设瓶子的容积为20，则混合后溶质和水的体积比为(15+16)∶(5+4)=31∶9。

3.十字交叉法

对于两种溶液混合的结果：某一溶液相对于混合后溶液，溶质增加；另一种溶液相对于混合后溶液，溶质减少。由于总溶质不变，因此增加的溶质等于减少的溶质，这就是十字交叉法的原理。

【示例】甲容器中有浓度为4%的盐水150克，乙容器中有某种浓度的盐水若干，从乙中取出450克盐水，放入甲中混合成浓度为8.2%的盐水，那么乙容器中的浓度是多少？

【解析】设乙容器内溶液浓度为x

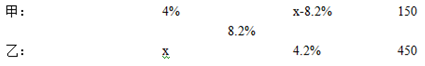
由(x-8.2%)/4.2%=150/450，解得x=9.6%

以上就是本文的全部内容，祝大家考试顺利~

推荐阅读：

事业单位有哪些

事业编事业单位报考条件要求

事业单位考试科目有哪些

事业单位考试内容

事业编制和公务员的区别

事业单位人事管理条例

事业单位联考各省试卷一样吗

事业单位联考什么意思

事业单位ABCDE类的区别是什么