事业单位《职测》数量关系备考技巧：方程法

在之前的文章中小编给大家介绍了事业单位《职测》数量关系中浓度问题的原理及解题思路，今天小编给大家准备了利用方程法来解决事业单位《职测》数量关系问题的适用范围及示例汇总，希望对备考的小伙伴们有所帮助。

一、定义及适用范围

1.定义

方程法是指将题目中未知的数用变量（如x，y）表示，根据题目中所含的等量关系，列出含有未知数的等式（组），通过求解未知数的数值来解应用题的方法。

2.适用范围

方程法应用范围较为广泛，数学运算绝大部分题目，如行程问题、工程问题、盈亏问题、和差倍比问题、浓度问题、利润问题、年龄问题等均可以通过方程法来求解。

二、分类示例

1.N元一次方程（组）

主要流程为：设未知量→找出等量关系→列出方程（组）→化简、解出方程

【例1】商店经销某商品，第二次进货的单价是第一次进货单价的九折，而售价不变，利润率比第一次销售该商品时的利润率增加了15个百分点，则该商店第一次经销该商品时所定的利润率是（ ）。

A.35%

B.20%

C.30%

D.12%

【解析】A。设第一次进价为100，售价为x，则

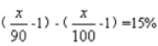
解得x=135，即第一次进货的利润率为35%。

【例2】某工厂有学徒工、熟练工、技师共80名，每天完成480件产品的任务。已知每天学徒工完成2件，熟练工完成6件，技师完成7件，且学徒工和熟练工完成的量相等，则该厂技师人数是熟练工人数的（ ）倍。

A. 6

B. 8

C. 10

D. 12

【解析】D。学徒工和熟练工完成的量相等，但学徒工和熟练工的效率之比为1:6=1:3，故学徒工和熟练工的人数之比为3:1。设熟练工为x人，则学徒工为3x人，设技师为y人，则有：（3x+x+y=80，2×3x+6x+7y=480）。解得x=5，y=60，故技师人数是熟练工的60÷5=12倍。

2.不定方程

不定方程是指未知数的个数多于方程个数，且未知数受到限制（如要求是有理数、整数或正整数等）的方程或方程组。在行测考试中，最常出现的是二元一次方程，其通用形式为ax+by=c，其中a、b、c为已知整数，x、y为所求自然数。若出现三元或三元以上则可用整体代入消元去求所需要的量。

解不定方程时，我们需要利用整数的奇偶性、自然数的质合性等多种数学知识确定解的范围。

主要流程为：列出方程→化为标准形式→确定解的范围→根据解的范围进行试探

【例1】某公司的6名员工一起去用餐，他们各自购买了三种不同食品中的一种，且每人只购买了一份。已知盖饭15元一份，水饺7元一份，面条9元一份，他们一共花费了60元。问他们中最多有几人买了水饺?（ ）

A.1

B.2

C.3

D.4

【解析】C。设买盖饭、水饺和面条的人数分别是x、y、z，则依题意可得：（x+y+z=6，15x+7y+9z=60），可得4x+z=9。由于x、y和z都是整数，所以（x=1，z=5）或（x=2，z=1），两种情况y分别为0和3，所以买水饺最多为3人。

【例2】农民小李到农贸市场卖水果，苹果、梨、橘子、桃四种水果各一箱。苹果、梨、橘子三箱水果，平均每箱51个；梨、橘子、桃三箱水果，平均每箱47个；苹果、桃两箱水平，平均每箱43个。则苹果共有（ ）个。

A.41

B.45

C.49

D.53

【解析】C。设苹果、梨、橘子和桃分别为x，y，z和m。由题意可得：x+y+z=3×51=153，y+z+m=3×47=141，x+m=2×43=86），可得x=49，即苹果共有49个。

以上就是本文的全部内容，祝大家考试顺利~

推荐阅读：

事业单位有哪些

事业编事业单位报考条件要求

事业单位考试科目有哪些

事业单位考试内容

事业编制和公务员的区别

事业单位人事管理条例

事业单位联考各省试卷一样吗

事业单位联考什么意思

事业单位ABCDE类的区别是什么